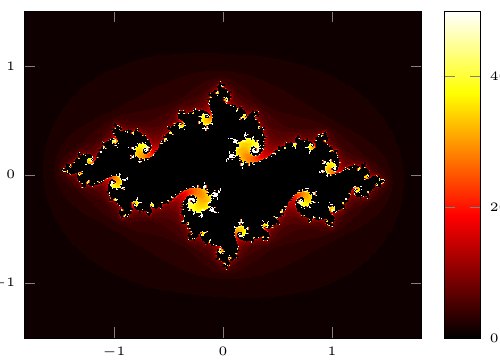
This is a picture of a Julia set, named after the French mathematician Gaston Julia. Computing requires a lot of iterations, that’s why we use Lua. The function for the set is z -> z^2 – 0.742 + 0.1i.
The example is very similar to the Mandelbrot example . One small difference is that we use a different color map.
Again, the sampling is done via \addplot3. surf and shader=interp do the coloring. Run with LuaLaTeX and have a coffee.
It was posted on: Fraktale mit pgfplots
Compiling this example takes too long for TeXlive.net, so you may get a timeout error.
%!TEX lualatex
\documentclass[border=5pt]{standalone}
\usepackage{pgfplots}
\pgfplotsset{width=7cm,compat=1.8}
\usepackage{luacode}
\begin{luacode}
function julia(cx,cy, max_iter, max)
local x,y,xtemp,ytemp,squaresum,iter
squaresum = 0
x = cx
y = cy
iter = 0
while (squaresum <= max) and (iter < max_iter) do
xtemp = x * x - y * y - 0.742
ytemp = 2 * x * y + 0.1
x = xtemp
y = ytemp
iter = iter + 1
squaresum = x * x + y * y
end
local result = 0
if (iter < max_iter) then
result = iter
end
-- result = squaresum
-- io.write("" .. cx .. ", " .. cy .. " = " .. result .. " (iter " .. iter .. " squaresum " .. squaresum .. ") \string\n")
tex.print(result);
end
\end{luacode}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
colormap/hot2,
colorbar,
axis equal,
point meta max=50,
tick label style={font=\tiny},
view={0}{90}]
\addplot3 [surf, domain = -1.82:1.82, shader = interp,
domain y = -1.5:1.5, samples = 350]
{\directlua{julia(\pgfmathfloatvalueof\x,\pgfmathfloatvalueof\y,10000,4)}
};
\end{axis}
\end{tikzpicture}
\end{document}