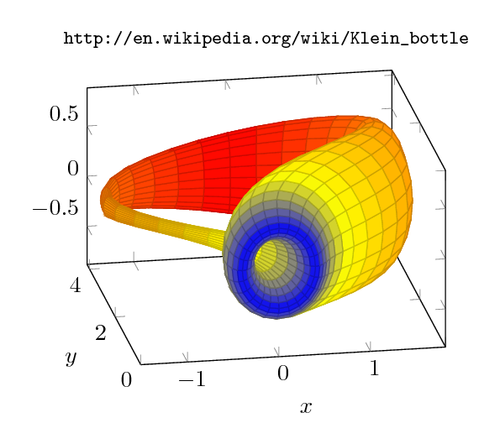
Both mesh and surface plots are actually special parametrized plots where x and y are on cartesian grid points. Parameterized plots just need a special way to provide the coordinates.
Her we plot the Klein bottle, which is an example of a non-orientable surface.
The code is from the PGFPlots 1.10 manual: “4.6.9 Parameterized Plots”. (GPL3+ license)
\documentclass[border=10pt]{standalone}
\usepackage{pgfplots}
\pgfplotsset{width=7cm,compat=1.8}
\usepackage{url}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
xlabel=$x$,
ylabel=$y$,
view/h=-10,
title=\footnotesize
\url{http://en.wikipedia.org/wiki/Klein_bottle},
]
\addplot3[
surf,
z buffer=sort,
colormap={periodic}{%
color=(blue)
color=(yellow)
color=(orange)
color=(red)
color=(orange)
color=(yellow)
color=(blue)},
domain=0:180, domain y=0:360,
samples=41, samples y=25,
variable=\u, variable y=\v,
point meta=u,
]
({-2/15 * cos(u) * (
3*cos(v) - 30*sin(u)
+ 90 *cos(u)^4 * sin(u)
- 60 *cos(u)^6 * sin(u)
+ 5 * cos(u)*cos(v) * sin(u))
},
{-1/15 * sin(u) * (3*cos(v)
- 3*cos(u)^2 * cos(v)
- 48 * cos(u)^4*cos(v)
+ 48*cos(u)^6 *cos(v)
- 60 *sin(u)
+ 5*cos(u)*cos(v)*sin(u)
- 5*cos(u)^3 * cos(v) *sin(u)
- 80*cos(u)^5 * cos(v)*sin(u)
+ 80*cos(u)^7 * cos(v) * sin(u))
},
{2/15 * (3 + 5*cos(u) *sin(u))*sin(v)});
\end{axis}
\end{tikzpicture}
\end{document}