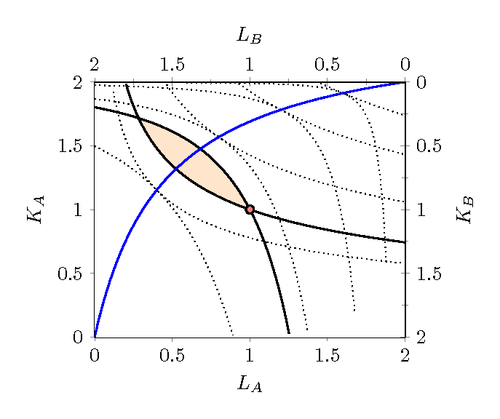
This edgeworth box describes the optimal allocation (pareto efficient) of inputs for the Cobb-Douglas production functions of two countries/regions (A and B). In addition, it shows the initial endowments of inputs and the resulting area of patero improvements. Parameters that can be changes: capital intensity parameter region A/B, total amount of labour and capital in A and B, and initial endowment K and L in A.
Edit and compile if you like:% Edgeworth box - Optimal allocation of inputs for two economies
% Author: Thomas de Graaff
\documentclass[border=10pt]{standalone}
\usepackage{pgfplots}
\pgfplotsset{width=7cm, compat=1.10}
\usetikzlibrary{calc, intersections} %allows coordinate calculations.
\begin{document}
\begin{tikzpicture}[scale=1,thick]
% Define parameters
\def\alpha{0.7} % Capital intensity parameter for region A.
\def\beta{0.3} % Capital intensity parameter for region B.
\def\L{2} % Total amount of labour in economy.
\def\K{2} % Total amount of capital in economy.
\def\PK{0.5} % Percentage K in A in initial endowment.
\def\PL{0.5} % Percentage L in A in initial endowment.
% Define isoquants
\def\InitYA{((\PL*\L)^(1-\alpha))*((\PK*\K)^(\alpha))}
\def\InitYB{(((1-\PL)*\L)^(1-\beta))*(((1-\PK)*\K)^(\beta))}
\def\La{0.2*\L}
\def\Lb{0.4*\L}
\def\Lc{0.6*\L}
\def\Ld{0.8*\L}
\def\Ka{%
\alpha*(1-\beta)*\K*\La/((1-\alpha)*\beta*(\L-\La)+\alpha*(1-\beta)*\La)}
\def\Kb{%
\alpha*(1-\beta)*\K*\Lb/((1-\alpha)*\beta*(\L-\Lb)+\alpha*(1-\beta)*\Lb)}
\def\Kc{%
\alpha*(1-\beta)*\K*\Lc/((1-\alpha)*\beta*(\L-\Lc)+\alpha*(1-\beta)*\Lc)}
\def\Kd{%
\alpha*(1-\beta)*\K*\Ld/((1-\alpha)*\beta*(\L-\Ld)+\alpha*(1-\beta)*\Ld)}
\def\YAa{((\La)^(1-\alpha)*((\Ka)^\alpha)}
\def\YAb{((\Lb)^(1-\alpha)*((\Kb)^\alpha)}
\def\YAc{((\Lc)^(1-\alpha)*((\Kc)^\alpha)}
\def\YAd{((\Ld)^(1-\alpha)*((\Kd)^\alpha)}
\def\YBa{((\L-\La)^(1-\beta)*((\K-\Ka)^\beta)}
\def\YBb{((\L-\Lb)^(1-\beta)*((\K-\Kb)^\beta)}
\def\YBc{((\L-\Lc)^(1-\beta)*((\K-\Kc)^\beta)}
\def\YBd{((\L-\Ld)^(1-\beta)*((\K-\Kd)^\beta)}
\begin{axis}[
restrict y to domain=0:\K,
samples = 100,
xmin = 0, xmax = \L,
ymin = 0, ymax = \K,
xlabel = $L_A$,
ylabel = $K_A$,
axis y line = left,
axis x line = bottom,
y axis line style = {-},
x axis line style = {-}
]
\def\LineA{(\InitYA/\x^(1-\alpha))^(1/\alpha))};
\def\LineB {\K-(\InitYB/(\L-\x)^(1-\beta))^(1/\beta)};
% color the area with all pareto improvements
\addplot [fill=orange!40, opacity=0.5, draw=none,domain=0:\L] {\LineB}
\closedcycle;
\addplot [fill=white, draw=none,domain=0:\L] {\LineA} |- (axis cs:0,0)
-- (axis cs:0,\K)--cycle;
%Draw isoquants
\addplot[thin, dotted, mark=none, domain=0:\L]
{(\YAa/\x^(1-\alpha))^(1/\alpha)};
\addplot[thin, dotted, mark=none, domain=0:\L]
{(\YAb/\x^(1-\alpha))^(1/\alpha)};
\addplot[thick, mark=none, domain=0:\L] {(\LineA};
\addplot[thin, dotted, mark=none, domain=0:\L]
{(\YAc/\x^(1-\alpha))^(1/\alpha)};
\addplot[thin, dotted, mark=none, domain=0:\L]
{(\YAd/\x^(1-\alpha))^(1/\alpha)};
\addplot[thin, dotted, mark=none, domain=0:\L]
{\K-(\YBa/(\L-\x)^(1-\beta))^(1/\beta)};
\addplot[thin, dotted, mark=none, domain=0:\L]
{\K-(\YBb/(\L-\x)^(1-\beta))^(1/\beta)};
\addplot[thick, mark=none, domain=0:\L] {\LineB};
\addplot[thin, dotted, mark=none, domain=0:\L]
{\K-(\YBc/(\L-\x)^(1-\beta))^(1/\beta)};
\addplot[thin, dotted, mark=none, domain=0:\L]
{\K-(\YBd/(\L-\x)^(1-\beta))^(1/\beta)};
% Draw contractcurve
\addplot[mark=none, domain=0:\L, color=blue,thick]
{\alpha*(1-\beta)*\K*\x/((1-\alpha)*\beta*(\L-\x)+\alpha*(1-\beta)*\x)};
% Draw initial endowments
\addplot[thick, mark=*, fill=red!50] coordinates {(\L*\PL,\K*\PK)};
\end{axis}
% Draw mirrored axis
\begin{axis}[
restrict y to domain = 0:\K,
minor tick num = 1,
xlabel = $L_B$,
ylabel = $K_B$,
xmin = 0, xmax = \L,
ymin = 0, ymax = \K,
axis y line = right,
axis x line = top,
x dir = reverse,
y dir = reverse,
y axis line style = {-},
x axis line style = {-}
]
\end{axis}
\end{tikzpicture}
\end{document}