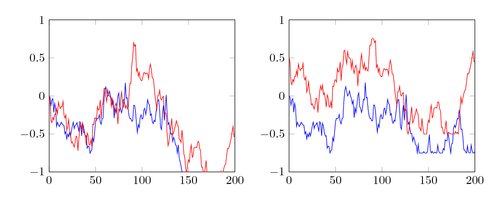
Here’s an approach using pgfplotstable to calculate the Brownian motions as cumulative sums of random normally distributed values. You have to first initialize an empty table, using something like \pgfplotstablenew{200}loadedtable, and then you can draw the brownian motions using \addplot table [brownian motion] {loadedtable};.
You can set the initial value and the maximum and minimum values using \addplot table [brownian motion={start=0.5, min=-1, max=1}] {loadedtable};
This code was written by Jake on TeX.SE.
Edit and compile if you like:
\documentclass[border=10pt]{standalone}
\usepackage{pgfplots}
\pgfplotsset{width=7cm,compat=1.8}
\usepackage{pgfplotstable}
% Create a function for generating inverse normally distributed numbers using the Box–Muller transform
\pgfmathdeclarefunction{invgauss}{2}{%
\pgfmathparse{sqrt(-2*ln(#1))*cos(deg(2*pi*#2))}%
}
% Code for brownian motion
\makeatletter
\pgfplotsset{
table/.cd,
brownian motion/.style={
create on use/brown/.style={
create col/expr accum={
(\coordindex>0)*(
max(
min(
invgauss(rnd,rnd)*0.1+\pgfmathaccuma,
\pgfplots@brownian@max
),
\pgfplots@brownian@min
)
) + (\coordindex<1)*\pgfplots@brownian@start
}{\pgfplots@brownian@start}
},
y=brown, x expr={\coordindex},
brownian motion/.cd,
#1,
/.cd
},
brownian motion/.cd,
min/.store in=\pgfplots@brownian@min,
min=-inf,
max/.store in=\pgfplots@brownian@max,
max=inf,
start/.store in=\pgfplots@brownian@start,
start=0
}
\makeatother
% Initialise an empty table with a certain number of rows
\pgfplotstablenew{201}\loadedtable % How many steps?
\pgfplotsset{
no markers,
xmin=0,
enlarge x limits=false,
scaled y ticks=false,
ymin=-1, ymax=1
}
\tikzset{line join=bevel}
\begin{document}
\pgfmathsetseed{3}
\begin{tikzpicture}
\begin{axis}
\addplot table [brownian motion] {\loadedtable};
\addplot table [brownian motion] {\loadedtable};
\end{axis}
\end{tikzpicture}
\pgfmathsetseed{3}
\begin{tikzpicture}
\begin{axis}
\addplot table [
brownian motion = {%
max = 0.5,
min = -0.75
}
] {\loadedtable};
\addplot table [
brownian motion = {%
start = 0.5,
min = -0.5,
max = 0.75
}
] {\loadedtable};
\end{axis}
\end{tikzpicture}
\end{document}